![\includegraphics[]{fig/mesure_entropie.eps}](img125.png)
Légende:
``HEP'' Graphe de la relation entre
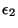 (abscisses)
et (abscisses)
et  (ordonnées), suivant différentes amplitudes d'un même type
de bruit de mesure. L'échelle logaritmique est appliquée pour les abscisses. (ordonnées), suivant différentes amplitudes d'un même type
de bruit de mesure. L'échelle logaritmique est appliquée pour les abscisses.
``DG'' Données issues de 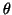 bruitées avec un bruit gaussien,
d'amplitude bruitées avec un bruit gaussien,
d'amplitude 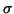 . .
``DVA'' Données issues de 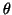 possédant un taux de valeurs
aberrantes possédant un taux de valeurs
aberrantes 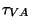 . .
``EA'' L'état du système peut être choisi aléatoirement, avec une
fréquence d'apparition 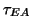 . .
Commentaires: Les points des graphes (a), (b) et (c) sont
obtenus en fixant une amplitude de bruit de mesure et en
récupérant les valeurs de  et de et de
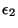 associées.
L'évolution de associées.
L'évolution de  est traitée dans la sous-section
1.4.4, alors que l'étude de est traitée dans la sous-section
1.4.4, alors que l'étude de
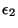 est donnée
dans la sous-section 1.4.5. Les droites sont obtenues
en utilisant le critère des moindres carrés, par l'algorithme de
Levenberg-Marquardt. Elles modélisent un lien fonction, pour
lequel est donnée
dans la sous-section 1.4.5. Les droites sont obtenues
en utilisant le critère des moindres carrés, par l'algorithme de
Levenberg-Marquardt. Elles modélisent un lien fonction, pour
lequel  peut s'exprimer en fonction de peut s'exprimer en fonction de
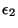 : :
 = a.log( = a.log(
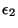 )+b. Dans ce cadre, on trouve, pour
les types de bruit DG, DVA et EA, les valeurs suivantes de a et b:
a=0.023, b=0.54; a=0.028, b=0.58; a=0.082, b=1.17. )+b. Dans ce cadre, on trouve, pour
les types de bruit DG, DVA et EA, les valeurs suivantes de a et b:
a=0.023, b=0.54; a=0.028, b=0.58; a=0.082, b=1.17.
|
![\includegraphics[]{fig/mesure_entropie.eps}](img125.png)