3 Spécification du problème posant le lien perception/mémorisation

Voici comment nous appréhendons le rapport entre la perception et la mémorisation. L'hypothèse 10 donne une condition nécessaire pour que le processus de perception engendre concrètement une observation (condition d'observabilité). Nous pouvons la traduire sous la forme du problème suivant: la personne cobaye observe une figure constituée de n points, dont les abscisses sont régulièrement espacés et les valeurs des ordonnées toutes comprises entre 0 et 1. La courbe visualisée peut, soit avoir été générée au hasard avec une loi de densité uniforme sur [0,1], soit avoir été générée grâce à une fonction, dont on a éventuellement bruité artificiellement les différentes valeurs. La question posée à la personne cobaye est de deviner laquelle des deux méthodes a été employée, sans que cette dernière ne connaisse au préalable la fonction génératrice. Essayez par vous-même de répondre à cette question dans les cas présentés par la figure 1.15. D'une manière objective, si on fixe un seuil de tolérance l $\in$ ]0, 1], la probabilité d'obtenir au hasard les points de la figure à l près est la même, quelle que soit cette figure (lorsque l est fixé). Cependant, la personne cobaye pensera qu'une figure a été générée au hasard si elle ne détecte pas de régularité précise dans celle-ci. Elle choisira l'option inverse si une régularité est découverte. Or, cette découverte dépend essentiellement de la manière dont la personne perçoit cette figure. En outre, plus le nombre de points de la figure est élevé et plus le contraste entre les deux choix est saisissant; car, si le nombre de points est trop faible, la personne cobaye ne pourra pas conclure avec certitude.

Figure: Relation entre perception et certitude d'une régularité.

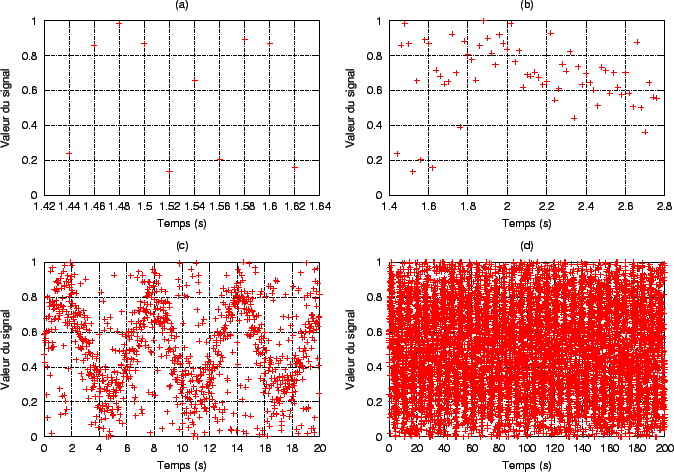
Les quatre figures sont issues du même signal. Pourtant, nous ne serions pas choqués si on nous avait affirmé que la figure (a) a été générée aléatoirement. Les figures (b) puis (c) laissent peu de doute: il est difficilement imaginable qu'elles soient issues d'un tirage aléatoire des valeurs sur [0,1]. La figure (d) montre qu'à une échelle de temps encore plus grande, le doute redevient total.

Nous avons mis en évidence deux facteurs qui vont guider le choix de la personne cobaye: le nombre de points de la figure, conditionnant la certitude avec laquelle la réponse est donnée, et l'utilisation de sa propre faculté de perception, qui dépend de la remémoration de son expérience perceptive passée. En particulier, si on se place dans un problème où la personne reçoit le flot de données d'un signal unidimensionnel à intervalles de temps régulier, le nombre de points est directement lié à une durée de perception. Voici comment nous allons utiliser ces deux facteurs pour construire un problème respectant les conditions imposées dans le paragraphe précédent ³². Nous allons supposer que le processus de perception de la personne cobaye est formé par une entité, que nous nommerons P. À chaque instant t, P reçoit la valeur d'un nouveau point de la figure. Au même moment, P essaie d'anticiper ce qui va être perçu, conformément à l'hypothèse 8; pour cela, il choisit un certain nombre de scenarii d'évolution possible de la suite de points sur une durée d fixée a priori, correspondant à l'obtention de h points. Ces scenarii peuvent être représentés par des ``tuyaux'' possédant chacun une section constante l, qui ont pour fonction de prévoir une évolution possible du signal sur les pas de temps t + 1, t + 2,..., t + h. On supposera qu'un scenario a effectivement prévu l'évolution des valeurs des points de la figure si au moins i points parmi n possibles se trouvent à l'intérieur du ``tuyau'' à l'instant t+d. Il s'agit là d'une contrainte, propre à chaque ``tuyau'', qui détermine s'il ``colle'' ou non à l'évolution des valeurs des points de la figure. Cette contrainte s'appliquant à chaque ``tuyau'' de l'univers des possibilités choisi à l'instant t permet de réduire ce dernier au cours du temps, en éliminant les ``tuyaux'' n'ayant pas respecté leur contrainte. La durée d correspond au temps minimal nécessaire à l'obtention d'une information ``certaine'' à propos de la nature de la figure. Par là, nous respectons bien l'hypothèse d'un traitement dynamique de la perception, et nous la justifions à l'aide de l'hypothèse 10.
Le chapitre 2 traite, entre autres, de ce processus d'élagage, dont la figure 1.16 montre schématiquement le principe. Ce processus utilise un paramètre, nommé $\epsilon$ dans la suite de ce mémoire, qui représente le degré d'incertitude associé aux actions de rejet ou de conservation des scenarii qui constituent le processus d'élagage. En outre, il est montré que si l'univers des possibilités choisi à l'instant t n'est pas trop ``gros'', on peut fixer les paramètres h,i de manière à ce que ce processus d'élagage conduise à ce qu'aucun ``tuyau'' ne soit solution à l'instant t+d avec une probabilité³³ 1 - $\epsilon$, si l'ensemble des points de la figure est choisi de manière aléatoire selon une loi uniforme sur [0,1] ³⁴. Nous admettons que la personne cobaye utilise inconsciemment l'entité P pour prendre sa décision: elle considérera que la figure a été générée aléatoirement si le processus d'élagage élimine l'ensemble des possibilités au bout d'une durée d (ce qui équivaut à h pas de temps).
Si nous nous intéressons au problème de choix de l'univers des possibilités initial (à l'instant t), qui est une partie de l'univers des possibilités total (équipotent à [0, 1]^h), nous constatons qu'il respecte les contraintes données dans le paragraphe précédent. La nature du problème est modifiée par rapport à celle donnée précédemment: choisir un ensemble de scenarii possibles d'évolution des valeurs des points sur h pas de temps, de manière à respecter les deux contraintes suivantes:

• la taille de l'ensemble des évolutions possibles n'est pas trop grosse par rapport à l'univers des possibilités total.
• le processus d'élagage n'élimine pas toutes les possibilités au bout d'une durée d, dans le cas où les points de la figure n'ont pas été générés d'une manière totalement aléatoire.

Dans ce problème, la ``personne'' cobaye est l'entité P. On constate dans ce cas que l'observateur peut fixer la taille de cet univers aussi grande qu'il le désire, en jouant sur le paramètre d'incertitude $\epsilon$, qui lui-même conditionne la valeur du paramètre h (voir le chapitre 2).
Voici comment nous interprétons les deux conditions données ci-dessus. L'ensemble des possibilités choisies par P forme un contexte perceptif. Si celui-ci est trop ``gros'', des ensembles de points choisis aléatoirement peuvent être sélectionnés après élagage, impliquant une réponse fausse de la personne cobaye. Au contraire, si cet ensemble est trop restreint et mal adapté à l'ensemble de points réellement présenté, l'élagage peut être total, alors que ces points n'ont pas été générés aléatoirement. Ces deux conditions définissent donc un compromis.
Nous pensons que l'implication de la mémoire dans le processus perceptif est justement de régler ce compromis. En d'autres termes, nous admettons que le processus de mémorisation permet de résoudre le problème de choix de l'entité P, évoqué ci-dessus.

Figure: Processus d'élagage

Le processus d'élagage (figure de gauche) élimine au cours du temps l'ensemble des ``tuyaux'' n'ayant pas respecté leur contrainte. La durée de ce processus est calculée d'une manière déterministe en fonction du degré d'incertitude $\epsilon$ et de l'univers des possibilités choisi à l'instant t par l'entité P. La figure de droite montre un tel ``tuyau'' pour h=5. Dans ce cas, 3 points sur 5 sont situés à l'intérieur du ``tuyau''; les contraintes sont respectées si i est inférieur ou égal à 2. Pour le détail du formalisme associé, voir le chapitre 2.