



suivant: Préparation du contexte d'apprentissage
monter: Problème de navigation d'un
précédent: Introduction
Table des matières
Le robot mobile miniature Khepera (figure 2.10)
est circulaire et mesure environ 5 cm de diamètre. Il possède 8 capteurs
infrarouge
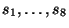 , dont la portée maximum est de 5 cm
, dont la portée maximum est de 5 cm
![[*]](file:/usr/lib/latex2html/icons/footnote.png) et dont les données sont significativement
bruitées. Ces capteurs renvoient des données codées sur 10 bits
(de 0, à 1023): ``0'' signifie que le capteur ne signale pas d'obstacle,
alors que ``1023'' signale un obstacle très proche. Il faut préciser à ce
sujet que la portée minimale du capteur est d'environ 2 cm. Le robot est
commandé en envoyant deux directives concernant les vitesses linéaires
et dont les données sont significativement
bruitées. Ces capteurs renvoient des données codées sur 10 bits
(de 0, à 1023): ``0'' signifie que le capteur ne signale pas d'obstacle,
alors que ``1023'' signale un obstacle très proche. Il faut préciser à ce
sujet que la portée minimale du capteur est d'environ 2 cm. Le robot est
commandé en envoyant deux directives concernant les vitesses linéaires
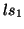 et
et 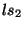 de ses roues. Vue la légèreté de ce robot et la
faible vitesse de déplacement, l'inertie de ce dernier est négligeable.
Pour de plus amples informations sur ce robot, le lecteur pourra
consulter [Mondada et al., 1994].
de ses roues. Vue la légèreté de ce robot et la
faible vitesse de déplacement, l'inertie de ce dernier est négligeable.
Pour de plus amples informations sur ce robot, le lecteur pourra
consulter [Mondada et al., 1994].
Figure 2.10:
Le robot miniature Khepera.
|
|
Pour notre expérience, nous avons utilisé l'environnement de simulation
de robot mobile Khepera, programmé par Michel [Michel, 1996]. Le simulateur
reproduit correctement les imperfections des mesures issues des capteurs,
rendant les résultats obtenus par le simulateur très proches de ceux du robot
réel (voir [Maaref et al., 1999] pour des résultats qualitatifs).
Le problème de navigation du robot simulé consiste à atteindre
un objectif en utilisant un comportement de suivi de mur (problème de
viabilité) lorsqu'un obstacle l'empêche d'aller directement vers celui-ci.
On suppose que les positions du robot et de l'objectif sont parfaitement
connues à tout moment. On suppose qu'il existe deux signaux de renforcement
permettant de résoudre le problème d'évitement, nommés 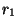 et
et 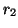 ,
dont les fonctions respectives sont de savoir si le robot s'est cogné
contre un obstacle et si le robot est resté trop longtemps éloigné d'un obstacle.
,
dont les fonctions respectives sont de savoir si le robot s'est cogné
contre un obstacle et si le robot est resté trop longtemps éloigné d'un obstacle.
La sous-section suivante présente une démarche de création de
contexte pour que le problème d'évitement puisse être résolu par
l'algorithme CbL. Comme il s'agit d'un problème de viabilité, nos
résultats théoriques indiquent qu'il suffit que le problème de
décision soit markovien; Nous noterons en particulier que le
contexte ne respecte pas (
 ).
).




suivant: Préparation du contexte d'apprentissage
monter: Problème de navigation d'un
précédent: Introduction
Table des matières
2002-03-01
![\includegraphics[]{fig/khepera_sim.eps}](img186.png)