Préparation du contexte d'apprentissage pour le problème de navigation du robot Khepera

L'ensemble des graphes de cette sous-section est donnée par la figure 2.11.

Figure: Graphes de la sous-section 2.6.3.

Dans le cadre d'un problème de viabilité, l'utilisation de l'algorithme CbL nécessite que le problème de décision soit markovien, c'est-à-dire que la probabilité de transition d'un état $e_{i,k}$ vers un état $e_{j}$ ne dépende que de $e_{i}$ et de $a_{k}$. L'échec de l'algorithme signifie soit qu'il n'existe pas de politique de commande fiable (à partir des états que nous avons constitués a priori), soit que le problème de décision n'est pas markovien.
Nous allons tout d'abord donner un premier contexte d'apprentissage, nommé $C_{1}$. Nous montrerons qu'il ne respecte pas la propriété ( $P_{\epsilon }$). Des résultats expérimentaux préliminaires (que nous ne donnons pas dans ce document) montrent que l'algorithme CbL échoue avec ce contexte. Nous présentons alors un deuxième contexte d'apprentissage, nommé $C_{2}$, utilisant une méthode de découpage hiérarchique de la tâche d'évitement. Nous montrons que l'algorithme CbL est alors capable de déterminer une politique de commande fiable, même si $C_{2}$ ne respecte pas la propriété ( $P_{\epsilon }$).
Dans cette sous-section, nous expliquons comment nous construisons les contextes $C_{1}$ et $C_{2}$ et nous prouvons que ceux-ci ne respectent pas la propriété ( $P_{\epsilon }$). Notre démarche est constituée des étapes suivantes:

1. déterminer la finesse du découpage sur chaque axe de l'espace d'entrée du système, qui est a priori de dimension 8
2. éliminer si possible les redondances entre les signaux d'entrée, de manière à réduire la dimensionnalité du problème
3. déterminer l'ensemble des commandes de base du robot

Imaginons que nous souhaitions partitionner l'espace d'entrée du système (qui est de dimension 8, puisque le robot est doté de 8 capteurs) en un ensemble de boîtes, tout comme dans l'exemple du pendule inversé (voir le chapitre 1). Le problème est de savoir comment il faut découper selon chacune des dimensions. Faut-il prendre un découpage fin où pas ? Le graphe (a) montre l'évolution du capteur $s_{1}$ dans le temps (graphe (a) ), lorsque le robot évolue dans l'environnement donné par le graphe (b). Nous constatons des sauts de valeur très brusques sur $s_{1}$. En conséquence, nous supposons qu'un découpage très grossier selon chaque axe de l'espace d'entrée est suffisant. Cela a déjà été constaté par [Maaref et al., 1999] entre autres, dans le cadre de la navigation d'un robot mobile Khepera utilisant un système d'inférence flou. Nous découperons en 4 suivant chaque axe. Ainsi, le découpage sera le suivant:

$$[0,1023] = [0,255] \bigcup [256,511] \bigcup [512,767] \bigcup [768:1023]$$

Malgré ce faible découpage, le nombre d'états est de $8^{4} = 4096$. Nous souhaitons réduire ce nombre. Pour cela, nous constatons que les valeurs associées à des capteurs voisins sont fortement corrélées: $s_{1}$ et $s_{2}$, $s_{3}$ et $s_{4}$, $s_{5}$ et $s_{6}$, puis $s_{7}$ et $s_{8}$. Nous allons réduire la dimensionnalité du problème en choisissant, pour chacune des paires de capteurs, le maximum des deux valeurs (c'est-à-dire le capteur donnant la plus courte distance). Les valeurs effectivement utilisées pour déterminer les états du système seront les suivantes:

$$d_{g} = \max\{s_{1}, s_{2}\}\:\:,\:\:d_{h} = \max\{s_{3}, s_{4}\}\:\:,\:\:d_{d} = \max\{s_{5}, s_{6}\}\:\:,\:\:d_{b} = \max\{s_{7}, s_{8}\}$$

Le nombre d'états est alors ramené à $4^{4} = 256$. Nous choisissons à présent l'ensemble des commandes de base du robot, c'est-à-dire un ensemble de couples ( $ls_{1}, ls_{2}$). Nous en avons sélectionné 5, nommées $a_{1},a{2},...,a{5}$ (voir le tableau 2.1 pour un descriptif), qui nous semblent suffisantes a priori pour accomplir la tâche d'évitement. L'ensemble des 256 états et des 5 commandes de base du robot constitue le contexte d'apprentissage $C_{1}$ de l'algorithme CbL.

Tableau: Commandes de base du robot Khepera simulé. Les valeurs de $ls_{1}$ et $ls_{2}$ sont sans unité.

Comportement	Signification	valeur de $ls_{1}$	valeur de $ls_{2}$
$a_{1}$	Tout droit	3	3
$a_{2}$	Avancer à droite	2	0
$a_{3}$	Avancer à gauche	0	2
$a_{4}$	Tourner sur la droite	2	-2
$a_{5}$	Tourner sur la gauche	-2	2

Le calcul des mesures $H_{1}$ et $H_{2}$ utilise l'algorithme 1.1, page . L'objectif est de découvrir l'ensemble des transitions possibles entres les états $e_{i,k}$ et les états $e_{j}$ du système. Ces transitions représentent les changements d'états possibles, suivant l'exécution des 5 commandes de base. Pour que $H_{1}$ et $H_{2}$ soient représentatives de l'ensemble de ces changements, il est nécessaire de placer le robot dans des environnements différents: nous en avons utilisé 10. Pour chacun de ceux-ci, nous effectuons 30 essais (voir l'algorithme 2.3). À la fin de chaque essai, on calcule les valeurs de $H_{1}$ et $H_{2}$. L'ensemble de ces valeurs forme les graphes (c) (pour $H_{1}$) et (d) (pour $H_{2}$). On constate que la propriété ( $P_{\epsilon }$) (voir la sous-section 1.3.4, page ) n'est pas satisfaite, car les valeurs de $H_{1}$ et de $H_{2}$ ne sont pas proches de 0: la courbe de $H_{1}$ semble posséder une limite supérieure proche de 0.2. La courbe de $H_{2}$ s'approche très rapidement de la valeur 0.4 . La courbe de $H_{1}$ est caractérisée par des ``sauts'' qui représentent l'expérience d'une nouvelle zone de l'espace d'états.


Le découpage hiérarchique a pour objet de transformer le contexte d'apprentissage du réflexe d'évitement en sous-contextes plus facilement apprenables. Cela revient à considérer un ensemble de sous-graphes construits à partir du graphe d'états induit par $C_{1}$, de manière à diminuer le nombre de transitions partant d'un état $e_{i,k}$. Cela suppose que la nature de la transition entre $e_{i,k}$ et $e_{j}$ n'est pas objectivement aléatoire, mais qu'elle dépend essentiellement d'un contexte. Le graphe (i) donne un exemple pour lequel le problème de transitions multiples peut être résolu en considérant deux contextes différents.


Le découpage de la tâche globale (atteinte d'une objectif en évitant les obstacles) s'organise tout d'abord autour de deux grandes catégories de processus:

1. les processus pouvant être programmés ``à la main'', sans avoir à utiliser une méthode d'apprentissage
2. les processus devant être appris

Dans notre cas, nous supposons que la position de l'objectif, la position du robot et son orientation par rapport à un repère fixe sont connus parfaitement à tout moment: le processus consistant à diriger le robot vers l'objectif peut donc être programmé très facilement. Il reste le processus d'évitement par suivi de mur: il sera appris. Celui-ci est découpé en sous-tâches, qui seront apprises par des agents appelés CbMU (pour Constraint based Memory Unit). Ces agents sont spécialisés de manière à réduire autant que possible leur nombre d'états. Les tâches à apprendre (décrites dans le tableau 2.2) sont hiérarchiquement connectées, suivant la figure 2.12. Chaque tâche est considérée comme un module indépendant, activé par une tâche hiérarchiquement supérieure. Lorsqu'un agent est activé, il choisit une des actions disponibles suivant la valeur courante des signaux perceptifs, puis reçoit en réponse un signal de renforcement qui lui est spécifique. Chaque tâche est réalisée par un agent CbMU, utilisant l'algorithme d'apprentissage CbL. L'ensemble des modules participe donc au comportement global d'évitement d'obstacle qui, à chaque pas de temps, revient à exécuter l'une des cinq actions élémentaires. Ce comportement global est utilisé par un algorithme de haut niveau d'atteinte d'objectif (algorithme 2.4), composé d'une base de règles, dont les prémisses utilisent les valeurs des marquages (obtenues grâce à l'apprentissage) des différents modules. L'objectif de ces règles est de constituer un branchement permettant de décider, à tout moment, si on peut se diriger vers l'objectif en toute sécurité, ou s'il faut adopter un comportement de suivi de mur. Il faut noter que la création d'une transition dans un graphe associé à une CbMU n'est possible que si celle-ci est activée (appelée par un supérieur hiérarchique ou par l'algorithme de haut niveau 2.4).

Tableau: Description des agents CbMU participant à la tâche globale d'évitement

CbMU	Description de la tâche	signaux d'entrée	commandes possibles	contrainte associée
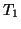$T_{1}$	Suivi mur gauche	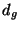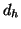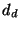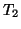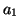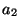$d_{g}$,$d_{h}$,$d_{d}$	$T_{2}$,$a_{1}$,$a_{2}$	NPSC,MG
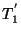$T_{1}^{'}$	Suivi mur droite	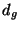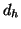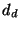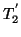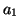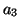$d_{g}$,$d_{h}$,$d_{d}$	$T_{2}^{'}$,$a_{1}$,$a_{3}$	NPSC,MD
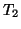$T_{2}$	Suivi mur convexe gauche	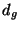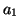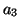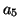$d_{g}$	$a_{1}$,$a_{3}$,$a_{5}$	NPSC,MG
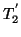$T_{2}^{'}$	Suivi mur convexe droite	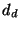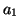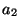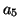$d_{d}$	$a_{1}$,$a_{2}$,$a_{5}$	NPSC,MD

NPSC: ``Ne pas se cogner'', ``MG'': être assez près d'un mur sur sa gauche, ``MD'': être assez près d'un mur sur sa droite.

Figure: Hiérarchisation des agents utilisés par Khepera dans son comportement d'évitement d'obstacles

Les flèches signifient ``peut utiliser''. Ainsi, la tâche $T_{1}$ (suivi de mur sur la droite) est une séquence de trois tâches plus élémentaires: $a_{1},a_{2}$ et $T_{2}$. $a_{1}$ et $a_{2}$ sont non décomposables. Par contre, $T_{2}$ (évitement d'obstacle sur la gauche) est une séquence des trois actions élémentaires $a_{1},a_{3}$ et $a_{5}$.

Nous venons donc de fixer $C_{2}$, qui est composé d'un ensemble de sous-contextes dans lesquels évoluent quatre agents CbMU. Nous allons à présent calculer les valeurs de $H_{1}$ et de $H_{2}$ pour les CbMU $T_{1}$ et $T_{2}$. Les deux autres étant leur ``symétrique'', elles sont a priori associées aux mêmes valeurs de $H_{1}$ et de $H_{2}$. Pour cela, nous effectuons la même démarche que précédemment, en choisissant au hasard: 1) la tâche d'évitement à accomplir, parmi $T_{1}$ et $T_{1}^{'}$, 2) en choisissant l'action à exécuter au hasard; si celle-ci consiste à activer une autre CbMU (tâches $T_{2}$ ou $T_{2}^{'}$), on choisit pour cette dernière l'action à exécuter au hasard. Les résultats sont présentés dans les graphes (e) et (f). On remarque que le découpage de la tâche principale (évitement en suivant un mur à droite ou à gauche) ne permet pas de réduire les valeurs de $H_{1}$ et de $H_{2}$. Par contre, on constate que la vitesse de ``convergence'' de $H_{1}$ et de $H_{2}$ vers leur valeur maximale est sensiblement plus rapide grâce au découpage. Cela signifie que l'ensemble des transitions possibles pour chacun des contextes des CbMU est plus rapidement trouvé. Or, on sait que la vitesse de convergence de l'algorithme CbL dépend uniquement de la rapidité avec laquelle le système ajoute des transitions dans le graphe perceptif. Donc, avant d'avoir effectué l'apprentissage, on peut prédire que la convergence de l'apprentissage sera plus rapide dans le contexte $C_{2}$ que dans $C_{1}$.